MÉTODO RACIONAL DE SOLFEO
(ENTONACIONES Y MEDIDAS)
Obligación nuestra es, facilitar la tarea a los estudiantes de música de las generaciones que nos sucedan.
Julián Carrillo.
Por la primera vez en la historia de la música, se hace un esfuerzo por incorporar totalmente su escritura a la cultura general.
Julián Carrillo.
EXORDIO
Durante siglos, se llamaron “Métodos de Solfeo”, a ciertos libros carentes de los atributos que les dieran derecho a llamarse “Métodos”; y que además, contenían una serie de ejercicios casi siempre desprovistos de musicalidad, y a ellos debíamos someternos los que estudiábamos en los conservatorios y en las academias. Todos esos llamados “Métodos”, estaban basados en un defecto que condena de un modo absoluto la pedagogía: iban de lo desconocido a lo desconocido.
Se empezaba por obligar a los estudiantes, a entonar melodías jamás oídas; por enseñarles a leer la música con signos jeroglíficos que jamás habían visto; y por último, a determinar la duración de los sonidos con procedimientos que nada decían al sentido del ritmo ni al del cálculo.
Eran pues, esos dizque “Métodos”, exponentes de problemas complejos, en forma irracional y antipedagógica, y por ello causaban pánico a los estudiantes de música. Semejante falta de “Método” en esos malamente llamados “Métodos” de “Solfeo”, ocasionaba que muchísimas personas –aun talentos de primer orden- abandonaran el estudio, con lo cual se ponía dique al esparcimiento de la música. Por lo expuesto se comprenderá, cuán urgente era una reforma fundamental en esos estudios, y no vacilé en intentarla, con lo cual, a la vez que contribuí a simplificar un problema que permaneció insoluto durante siglos, cumplí con mi deber como autor que soy de la Revolución Musical del Sonido 13.
Para lograr el fin propuesto, he abandonado los procedimientos arcaicos y rutinarios que se emplearon durante siglos para escribir, entonar y medir los sonidos. La primera reforma consistió, en no emplear ya el papel especial para escribir la música, sino el de rayas ordinario; la segunda, en suprimir todas las llaves, con lo cual se ahorran a los estudiantes y a los músicos en general, muchos años de estudios y miles de esfuerzos mentales penosísimos e innecesarios, y por último, no emplear ya los accidentes: bemoles, sostenidos, becuadros, dobles bemoles y sostenidos dobles, ni los accidentes mixtos: sostenidos y bemoles.
Esta reforma significa el ahorro de preciosa energía humana, que se desperdició en el mundo entero durante siglos.
Al suprimir todos esos signos, logro algo que la humanidad agradecerá algún día: la incorporación total de la escritura de la música a la cultura general.
Quien sepa contar de cero a once podrá escribir todos los sonidos musicales, y quien sepa sumar, podrá determinar con exactitud matemática la duración de ellos.
En cuanto a la afinación, quien conozca el Himno Nacional de su país tendrá bastante para el caso.
Siendo esta la base para el aprovechamiento pleno de mi “Método”, cabe preguntar: ¿cuál será el país en el que los ciudadanos ignoren su Himno Nacional?
Para melodías que sean desconocidas al estudiante de música, suficiente será que tenga a mano cuando empiece sus estudios, el “CARRILLÓFONO” inventado por mí, instrumento tan pequeño, que puede llevarse en un estuche de viaje; y con él, podrá oír cuantas veces le plazca los sonidos musicales perfectamente afinados.
No se crea que los procedimientos que aquí expongo sean únicamente para música sencilla, no; pues con ellos se pueden entonar con facilidad extraordinaria las obras más complicadas de Bach, Haendel, Haydn, Mozart, Beethoven, Wagner, Brahms, Debussy, Ricardo Strauss, Stravinsky y Schoenberg.
Como demostración de lo fácil que es el sistema de escritura que aquí presento, debo decir, que mis alumnos han transcrito ya a la nueva gráfica, con increíble rapidez y sin esfuerzo, obras de las más complicadas de los autores citados.
En cuanto a las figuras con que se representan los diversos valores de los sonidos, he logrado un resultado extraordinario: determinar matemáticamente su duración, evitando así lo que pasa hoy: emplear figuras largas para duraciones cortas y viceversa: valores cortos para duraciones largas, lo que es irremediablemente ilógico; defecto éste, en el que cayeron hasta los compositores más eminentes.
Con mi procedimiento, bastará abrir un libro de música, para darse cuenta en el acto, si la obra es de carácter rápido o lento.
Si abundan en la composición figuras largas, la obra será lenta; y si por el contrario, están en mayoría las de corta duración, la composición será rápida.
Acabé con este defecto universal, sirviéndome de un procedimiento matemático sencillísimo; asigno a la figura más larga, o sea la unidad –llamada ilógicamente semibreve o redonda-la duración invariable de cuatro segundos; a la mitad de ella, o sea la llamada blanca o mínima, dos segundos; a la cuarta parte, -llamada semínima o negra- un segundo; a su octava –llamada corchea- medio segundo; a la dieciseisava –llamada semicorchea por unos y doble corchea por otros- un cuarto de segundo; a la treintaidosava –llamada triple corchea por unos y fusa por otros- un octavo de segundo; y a la sesentaicuatroava parte –llamada cuádruple corchea por unos y semifusa por otros- un dieciseisavo de segundo.
Tengo ya en preparación un nuevo metrónomo, al que llamo “CARRILLÓMETRO”, de acuerdo con estos valores.
Tales son las reformas que implanto en mi “Método”; y en cuanto a los preceptos pedagógicos me basta observar uno que los compendia a casi todos: IR DE LO CONOCIDO A LO DESCONOCIDO, es decir: empezar con los sonidos de una melodía conocida: el himno nacional del país en el cual se implante mi Método (tal cosa significa que aunque la teoría sea la misma para todos los países, la base melódica y armónica será diferente, como diferentes son los himnos nacionales); emplear signos conocidos para escribirlos –del cero al once-; y medios igualmente conocidos para medirlos: los que se aprenden en la Escuela Primaria.
No titulé a mi libro “Método de Solfeo” a secas, porque esa palabra provenía según se asegura, de las notas Sol y Fa, y como en mi revolución musical han desaparecido las notas y sus nombres, no existen ya Sol ni Fa, y habría sido inconsecuente por lo mismo, seguir empleando un término que carecía de sentido etimológico. Tal es la razón por la cual doy a estos estudios el nombre de “Método de Entonaciones y Medidas”, supuesto que con los procedimientos que expongo, se aprenderá a entonar y medir los sonidos de la música sin el menor esfuerzo, y aun veo la posibilidad de que no sea necesario un maestro; pues con el “Carrillófono” como guía para entonar y con el “Carrillómetro” para medir, se sabrá con exactitud absoluta la altura y duración de los sonidos. Bastarán los medios indicados, para poder aprender música aun en pueblos montañeses a los que jamás llegan los músicos.
Tomo como punto de partida para el aprendizaje de la música en cada país, su Himno Nacional y así, no habrá persona alguna que no conozca desde su niñez los sonidos en que baso estos estudios, y al mismo tiempo será fácil darles su exacta duración.
Posible sería, y con mínimo esfuerzo, que los estudiantes del extranjero aprendieran de oído, la melodía del Himno Nacional Mexicano, base de este “Método”, y que con ello sería ya innecesario escribir un libro para cada país.
El autor llega a creer, inmodestamente, que este librejo prestará un servicio positivo en todo el mundo para el estudio de la música, y consideraría como un homenaje a su patria, que en las grandes naciones se estudiara la entonación y la medida de los sonidos musicales con esta edición a base del Canto Patrio Mexicano.
Los países que tal hicieren, recibirían por anticipado los agradecimientos del Autor.
Para servirse del “Carrillófono”, del piano o del armonium, bastará bajar con el dedo la tecla marcada con el número correspondiente al sonido que se desee, para oírlo en el acto perfectamente afinado.
En el final de este libro va una tira numerada y que debe colocarse en cualquier piano, de la tecla 28 contando de izquierda a derecha, a la 64, pegándola sobre las teclas negras 29 y 62, y servirá para indicar el número que corresponde a cada sonido, fijándose si el número está debajo de la línea, en ella o sobre ella.
Sirvan de exordio estas cuantas palabras, y entraré en materia.
JULIAN CARRILLO
PRIMERA LECCIÓN
Como en la música actual sólo hay doce sonidos, los escribo con doce números, del cero al once.
EJEMPLO 1

Como se ve en el ejemplo anterior, los sonidos 1, 3, 6, 8, y 10, se escriben en la gráfica en uso, de dos maneras diferentes.
Para mayor claridad, pongo el ejemplo en otra forma:
EJEMPLO 2
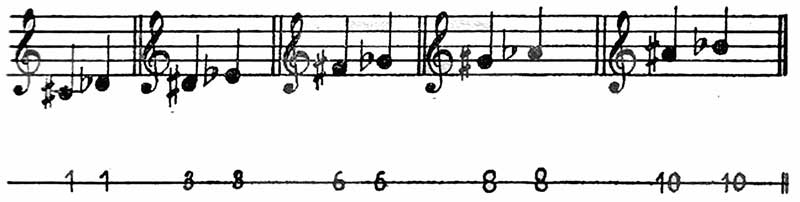
Esa doble manera de escribir los sonidos complica innecesariamente la lectura de la música.
(En mis libros “Pre-Sonido 13” y “Teoría Lógica de la Música”, señalo casos que demuestran que en el clasicismo hay hasta 54 maneras diferentes para escribir un solo sonido).
Mi criterio a este respecto es, que si son sólo doce los sonidos de la música, doce deben ser únicamente los signos que los representen.
Para aprender a entonar y medir los sonidos musicales, bastará servirse de la melodía del Himno Patrio.
He aquí el Himno Nacional Mexicano, en las dos escrituras: la clásica y la nueva.
EJEMPLO 3

Deberán los estudiantes practicar la primera parte del Himno Nacional (el coro) hasta que lo canten perfectamente afinado y medido.
Cántese diez o más veces la melodía que sigue, ya sea con la letra respectiva o tarareándola.
EJEMPLO 4
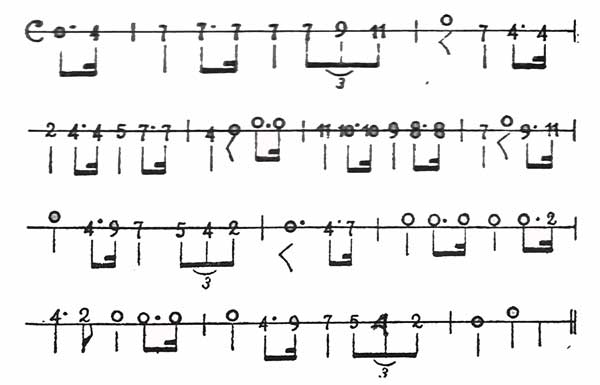
Los números al emplearlos para escribir los sonidos, indican relaciones de altura; es decir, que el 2 es más alto que el 1; que 3 es más alto que 2; 4 más alto que 3; etc.; y a la vez, se comprende sin esfuerzo, que de 1 a 2, la distancia es menor que de 1 a 3 ó de 1 a 4.
Deberá notarse que hay la misma distancia de 0 a 1 que de 1 a 2 y de 2 a 3, como de 4 a 5; en suma: la diferencia es la misma de cualquier número a su inmediato inferior o superior.
Cualquiera melodía puede cantarse en doce alturas diferentes, sin alterarla fundamentalmente.
Puede comprobar esta teoría, quien posea un “Carrillófono” (Instrumento de teclado a manera de pequeño piano, que produce los sonidos perfectamente afinados) o un piano o armonium tocando los sonidos de los ejemplos que siguen.
He aquí un fragmento del Himno Nacional, en doce alturas diferentes.
EJEMPLO 5

Como se ve, la melodía es la misma, no obstante que empieza con cualquiera de los doce números.
Con este simple procedimiento gráfico, se nulifican todas las teorías clásicas relacionadas con las tonalidades, lo que simplifica la teoría y la práctica de la música, en más de un cincuenta por ciento.
ACCIDENTES
Se llaman accidentes, a los bemoles, sostenidos, becuadros, dobles bemoles, sostenidos dobles, y a los bemoles y sostenidos mixtos.
Con mi nueva gráfica, quedan fuera de uso, todos esos problemas teórico-prácticos tan artificiosos como difíciles e innecesarios y que provienen de los mencionados signos.
Si les he dedicado unas cuantas palabras ha sido con el único propósito de que los que estudien mi “Método” no se sorprendan cuando les hablen de esos arcaísmos anticientíficos que se enseñan en todas las academias y conservatorios en el mundo entero.
Para terminar esta lección, aconsejo que se cante nuevamente la primera parte del Himno Nacional.
SEGUNDA LECCIÓN
Al empezar debe entonarse nuevamente el coro del Himno, para que se grabe más en la memoria de los estudiantes.
Cuantas veces puedan tocarse los sonidos en un instrumento perfectamente afinado el resultado será mejor.
En seguida comprobaremos –para que no quede duda alguna al estudiante- que las relaciones que hay de uno a otro sonido, no se alteran por el hecho de empezar con una u otra altura. El ejemplo 5 lo demuestra.
Las distancias que separan a los sonidos 0, 4, 7 son iguales en sus efectos a 1, 5, 8 y a 3, 7, 10; a 4, 8, 11, etc.
Como comprobación inmediata, aconsejo que se analicen los doce casos que indico en el ejemplo 5, y se verá que no obstante que cada uno empieza con diferente número, no se altera la melodía, debido a que las relaciones de los números son las mismas.
Tóquense en seguida en las doce alturas los sonidos del ejemplo que antecede, y se verá que más alta o más baja, la melodía es siempre la misma.
Si se amplía un poco el ejemplo anterior, tendremos:
EJEMPLO 6
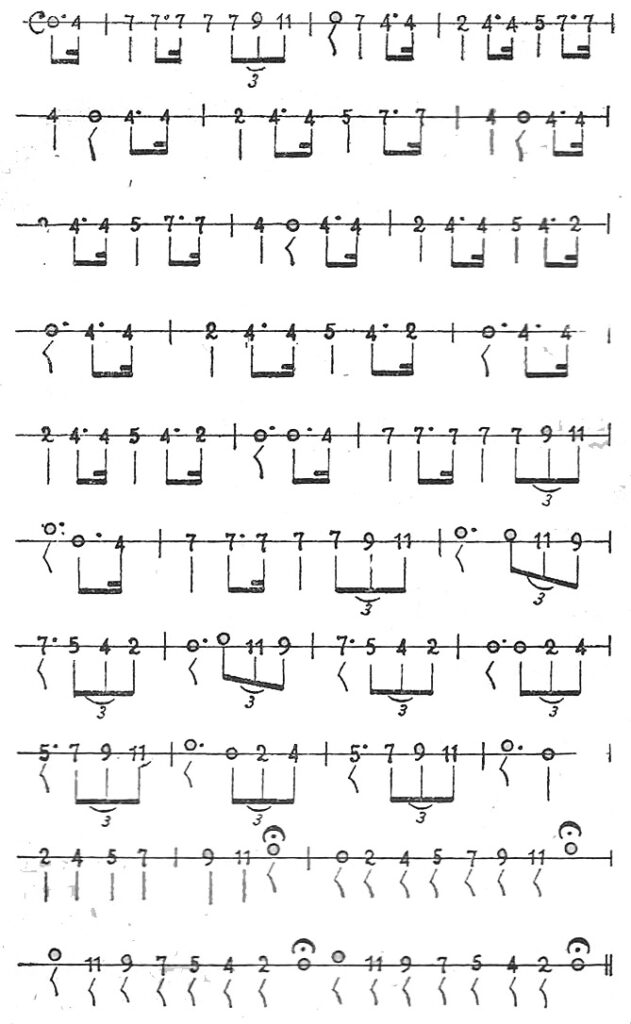
En este ejemplo hay un signo en forma de media luna con un punto debajo; tal signo significa que debe prolongarse la duración del sonido o del silencio sobre el cual está, y se llama “Calderón”.
Para que el alumno practique no sólo las entonaciones de los sonidos, sino también la escritura de ellos, sugiero que se escriba el ejemplo anterior un número más alto; después dos, luego tres, y seguir así hasta que se haya escrito en las doce alturas.
Podemos ampliar más aún el ejemplo anterior para la práctica.
EJEMPLO 7
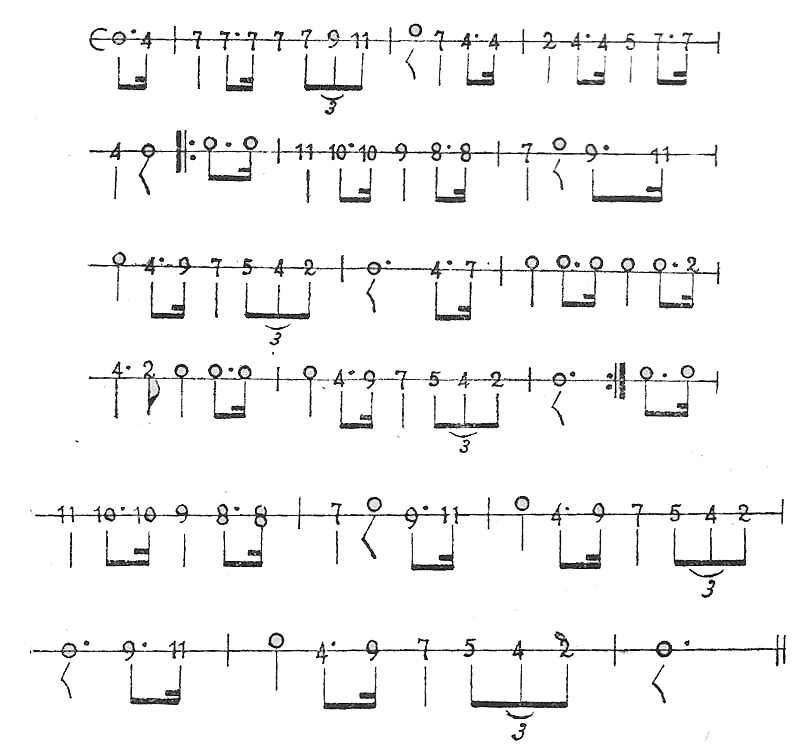
Una vez que el alumno haya escrito el ejercicio anterior en las doce diversas alturas, se dará por terminada la segunda lección, entonando una vez más la primera parte del Himno Nacional. se encuentran dobles barras divisorias de compás, y dos puntos a mitad de la altura de ellas, significa que debe repetirse lo que antecede, ya sea desde el principio de una composición o entre una parte de ella comprendida entre dobles barras y dobles puntos.
TERCERA LECCIÓN
Para empezar esta lección, entónese como en las anteriores, el Himno Nacional.
En seguida explicar a los estudiantes la melodía correspondiente a “Y retiemble en su centro la tierra”, y que es la del
EJEMPLO 8
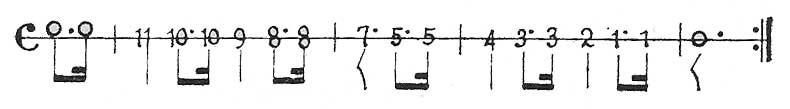
Una vez que se haya practicado suficientemente el ejemplo 8, practíquese en esta forma:
EJEMPLO 9
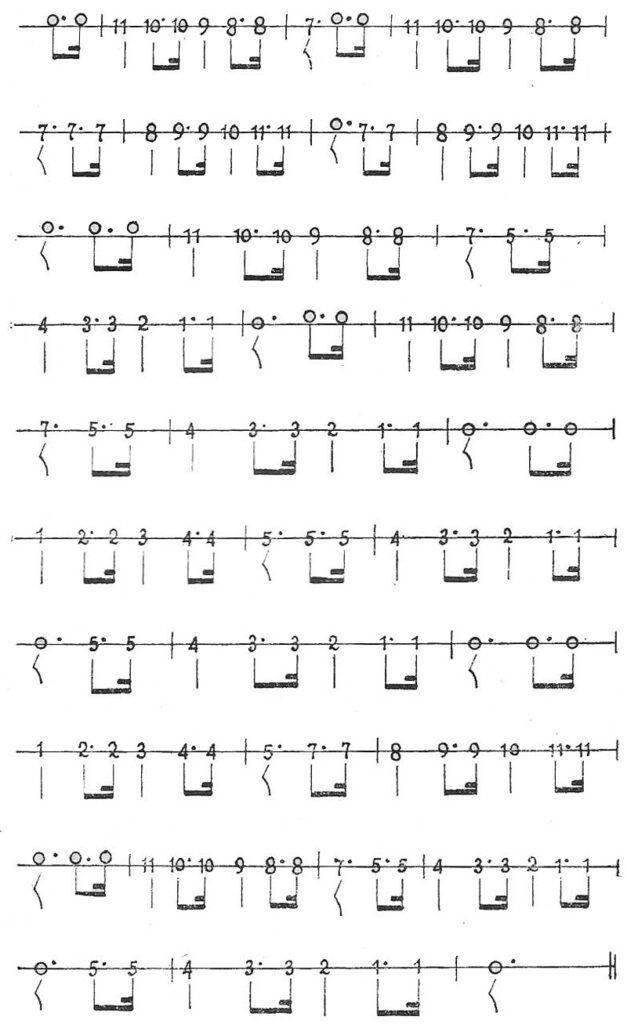
El estudiante deberá escribir ese ejemplo en las doce diversas alturas, y leerlo en cada una de ellas cantándolo, para convencerse de un modo absoluto, de que las relaciones indicadas por los números son las mismas, cualquiera que sea el sonido inicial.
Haremos en seguida un ejercicio más y que será de grandísima utilidad.
EJEMPLO 10
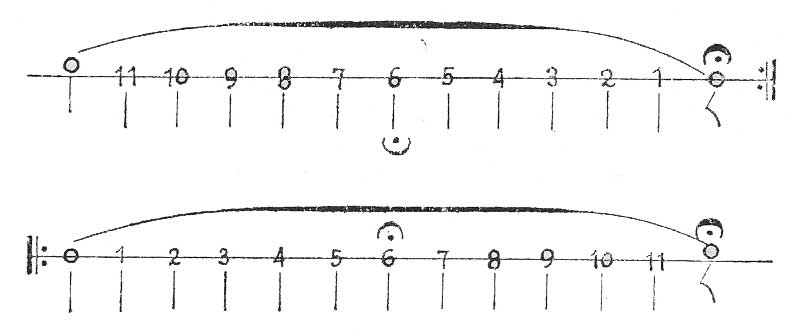
Cuando se escribe –como en el ejemplo anterior- una línea curva abarcando dos o más sonidos, esa línea se llama ligadura, e indica que no debe respirarse sino hasta que ella termine.
Como en los casos anteriores, el alumno debe escribir el ejemplo 11 en todas las alturas, es decir: empezar con cualquiera de los doce números y después entonarlo; primero en una altura, luego en otra, y así hasta que se practique en todas ellas.
EJEMPLO 11
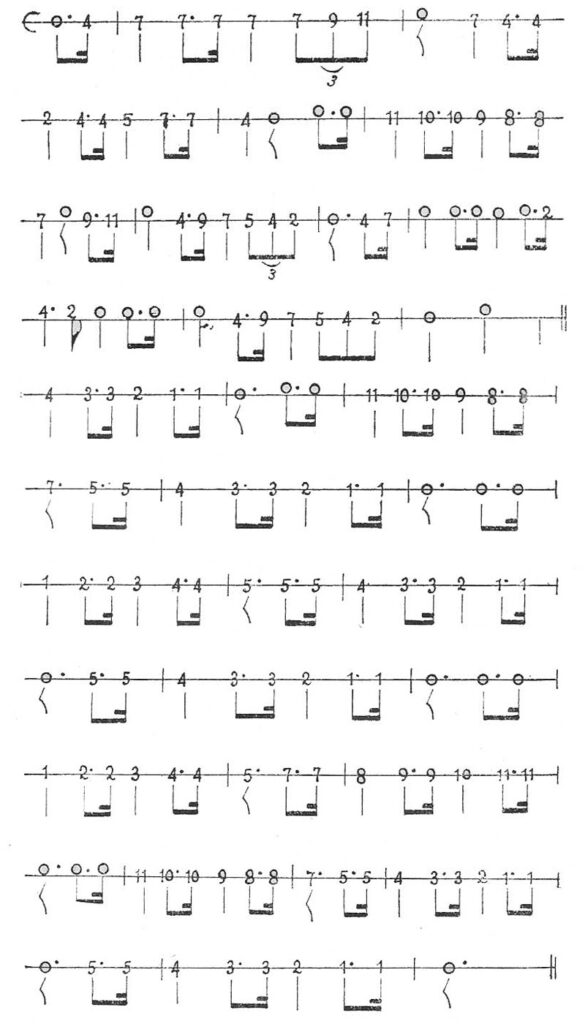
Para terminar la tercera lección, entónese el Himno Nacional, que será el medio para aprender a entonar y medir los sonidos sin el martirio de los signos jeroglíficos que nos legaron las generaciones de los siglos idos.
Como al conocerse este “Método” en todos los países civilizados, es seguro que lo estudiarán, con ello se logrará un resultado que exige la época que vivimos: que los himnos nacionales sean venerados y reverenciados.
CUARTA LECCIÓN
Entónese el Himno Nacional.
En seguida, indicaré la manera de escribir todos los sonidos de la música, que como dije ya, son sólo doce, pero que se repiten en ocho diversas alturas, y cada serie de esas alturas diversas, se llama ciclo.
Como no empleo ya la pauta clásica de la música, ni necesito las complicadísimas líneas adicionales, suplo todo eso con sólo una línea fija y dos guiones, con lo cual desaparecen todas las dificultades para leer tantas y tantas líneas en las pautas fijas y adicionales que se emplean para escribir la música según los procedimientos clásicos.
Para lograr ese resultado, me bastó aprovechar las tres alturas de cada línea horizontal, o sea: debajo, en y sobre. Con tan sencillo procedimiento puedo escribir hasta nueve ciclos, uno más de los hay en la música.
Escribo el ciclo más bajo, debajo del guión inferior:
EJEMPLO 12
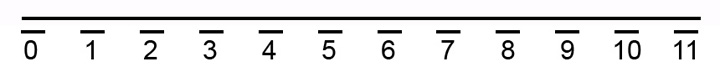
El segundo, en el guión inferior:
EJEMPLO 13
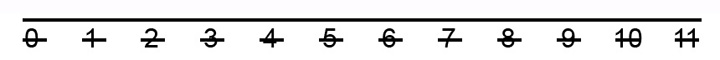
El tercero, sobre el guión inferior:
EJEMPLO 14
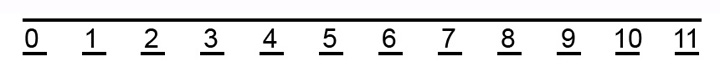
El cuarto, debajo de la línea fija:
EJEMPLO 15

El quinto, en la línea fija:
EJEMPLO 16
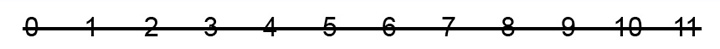
El sexto, sobre la línea fija:
EJEMPLO 17
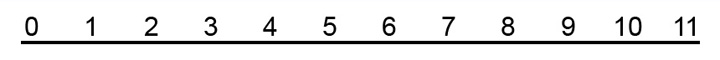
El séptimo, debajo del guión superior:
EJEMPLO 18
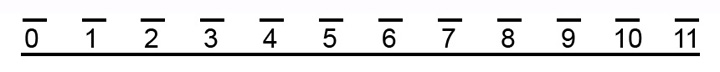
El octavo, en el guión superior:
EJEMPLO 19
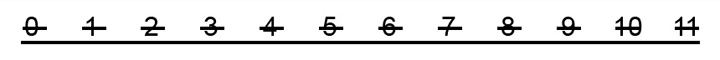
Y sobre el guión superior únicamente escribo un sonido –como se verá en el ejemplo que sigue- en atención a que no existe ningún instrumento capaz de alcanzar el noveno ciclo que puedo escribir sobre ese guión.
He aquí la extensión total de los pianos de concierto:
EJEMPLO 20
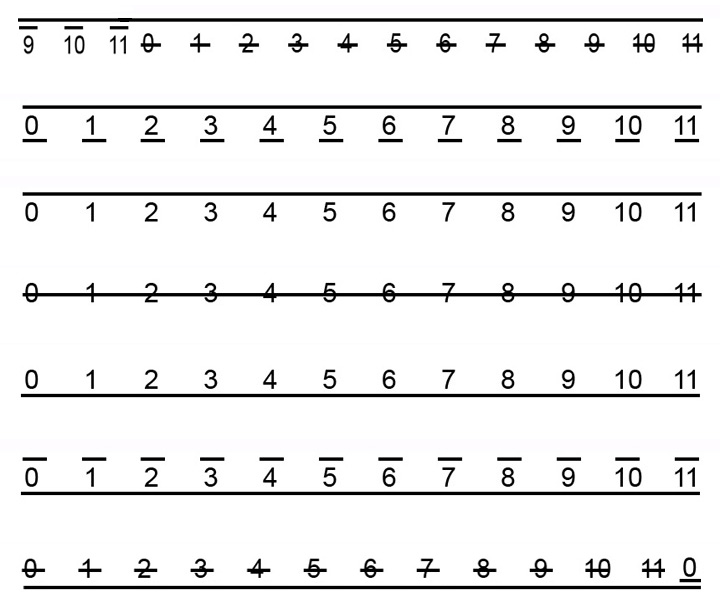
Como se ve, los sonidos del piano empiezan en el número 9 del primer ciclo.
INTERVALOS
Intervalo, científicamente, es la diferencia de vibraciones que hay entre dos sonidos en determinado lapso.
Los teóricos del clasicismo, empleaban para distinguir un intervalo de otro, la siguiente clasificación: subdisminuídos, disminuídos, menores, mayores, aumentados, superaumentados, justos, perfectos, consonantes y disonantes; clasificación anticientífica, ilógica y grotesca, y además dificilísima. Por todas esas razones la he desechado absolutamente.
Como no es verdad musical, física ni lógica, que existan intervalos disminuídos, ni subdisminuídos, menores, mayores, ni aumentados, superaumentados, justos, perfectos, consonantes ni consonancias imperfectas, baso mi clasificación en la física y la lógica, y con esto resulta sólo uno de cada especie. Uno de 2ª; otro de 3ª; uno de 4ª; otro de 5ª; uno de 6ª; y sólo uno de 7ª, de 8ª, de 9ª, de 10ª, de 11ª, de 12ava, de 13ava, de 14ava, etc.
Segunda es, entre dos números vecinos, como por ejemplo de 2 a 3, de 3 a 4, de 6 a 7, etc.
EJEMPLO A
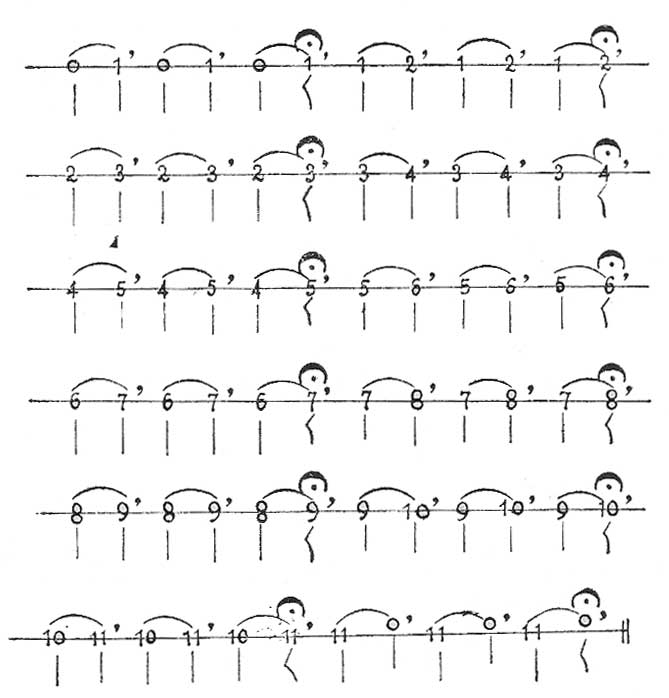
Tercera entre tres sonidos sucesivos 0, 1, 2; 1, 2, 3; 2, 3, 4; 3, 4, 5; y que al entonarse se salta uno, o sea; tercera de 0 a 2; de 1 a 3; de 2 a 4; de 3 a 5; etc.
EJEMPLO B
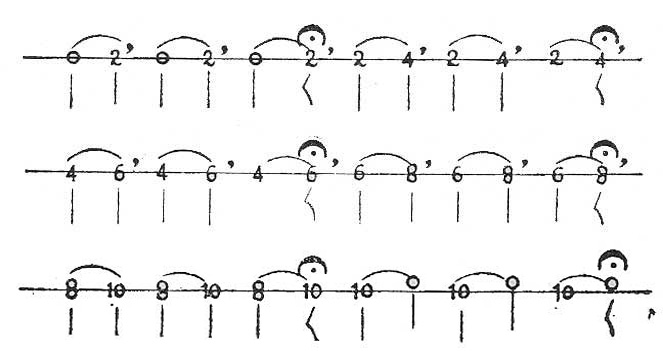
Cuarta, cuando son cuatro sonidos sucesivos 0, 1, 2, 3; 1, 2, 3, 4; etc., y que al cantarse se saltan dos, como por ejemplo, de 0 a 3, de 1 a 4, de 2 a 5 de 3 a 6, etc.
EJEMPLO C
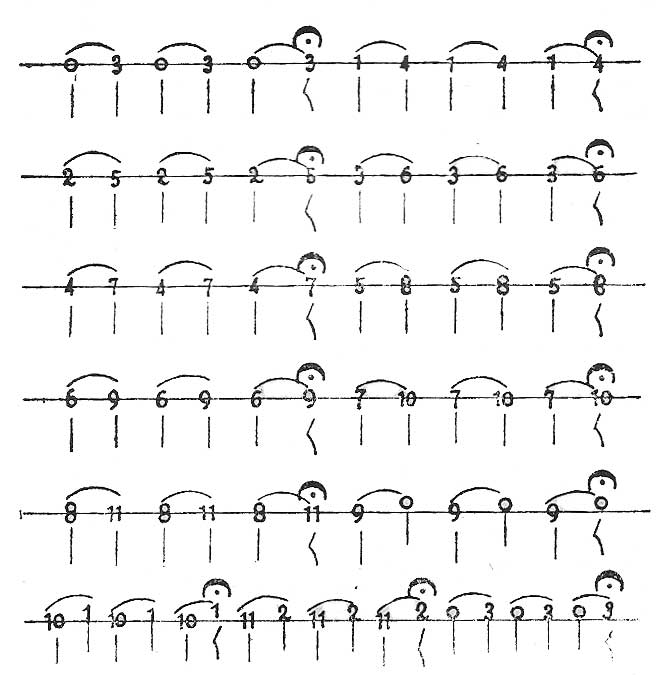
Quinta, cuando son cinco sonidos sucesivos: 0, 1, 2, 3, 4; 1, 2, 3, 4, 5, etc., y que al entonarse se saltan tres, como entre 0 y 4, entre 1 y 5; entre 2 y 6, etc.
EJEMPLO D
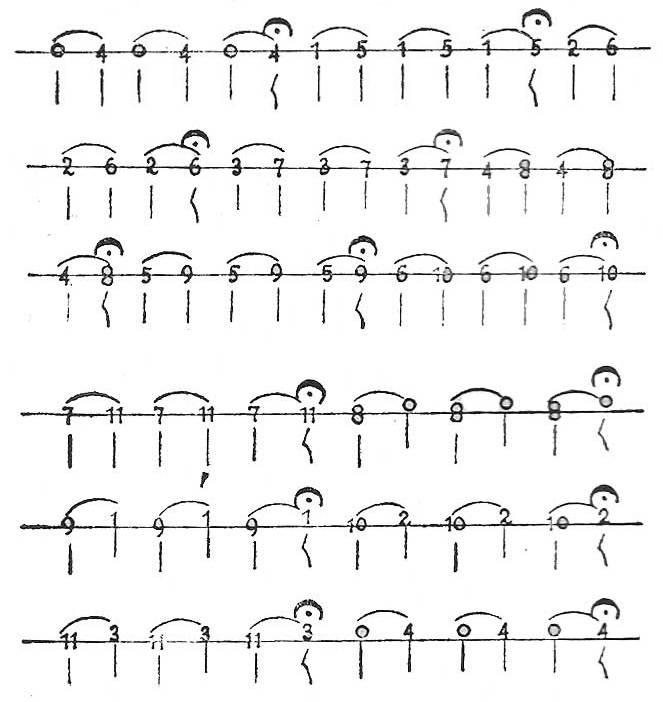
Sexta, entre seis sonidos sucesivos saltando cuatro; como de 0 a 5, de 1 a 6, de 2 a 7, de 3 a 8, etc.
EJEMPLO E
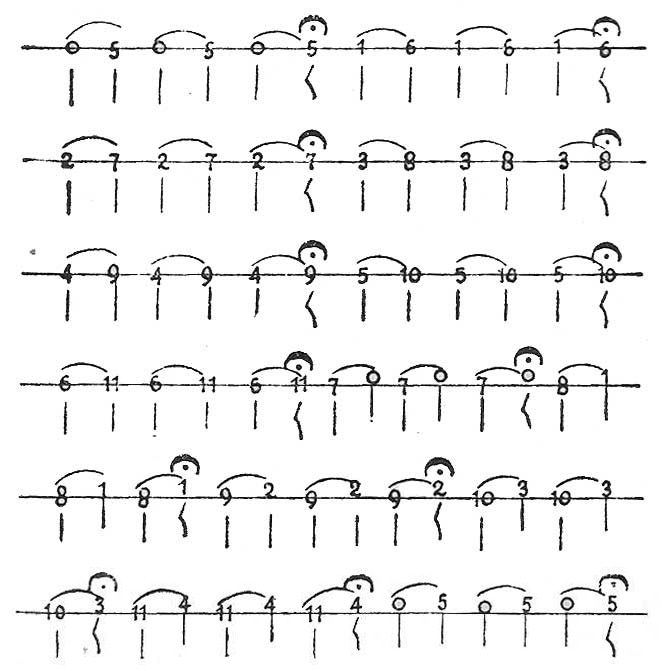
Séptima, entre siete sonidos, saltando cinco al cantarlos, tales como de 0 a 6, de 1 a 7, de 2 a 8, de 3 a 9, etc.
EJEMPLO F
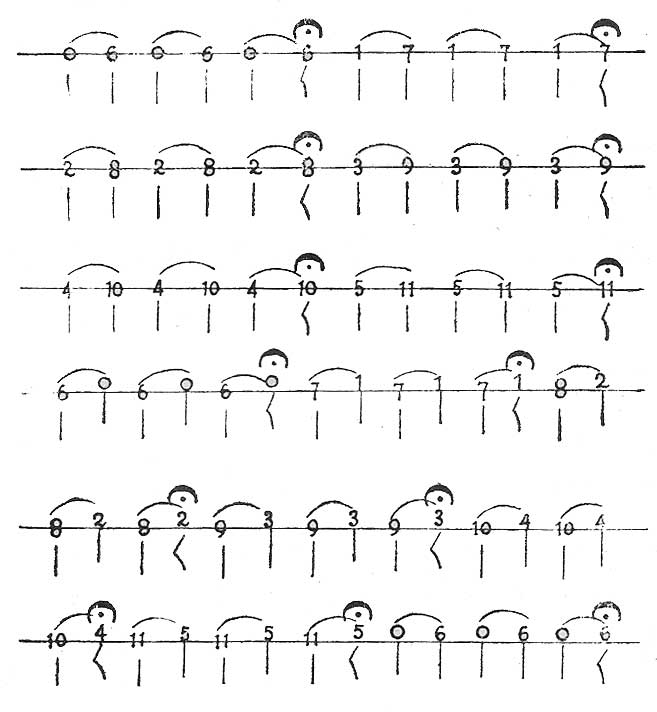
Octava, entre ocho sonidos sucesivos saltando seis, como de 0 a 7, de 1 a 8, de 2 a 9, de 3 a 10, etc.
Esta 8ª lógica, nada tiene que ver con la que ilógicamente llaman 8ª, los músicos que no cultivan mis teorías. El intervalo llamado por mí 8ª tiene ocho sonidos, y la dizque 8ª de los músicos tiene 13. Sólo los músicos enemigos (¿?) de la revolución del Sonido 13, tal vez por que esta es lógica pura, pueden creer que 8ª son trece sonidos; pues cualquiera persona de sentido común sabe que 8ª son únicamente ocho sonidos.
EJEMPLO G
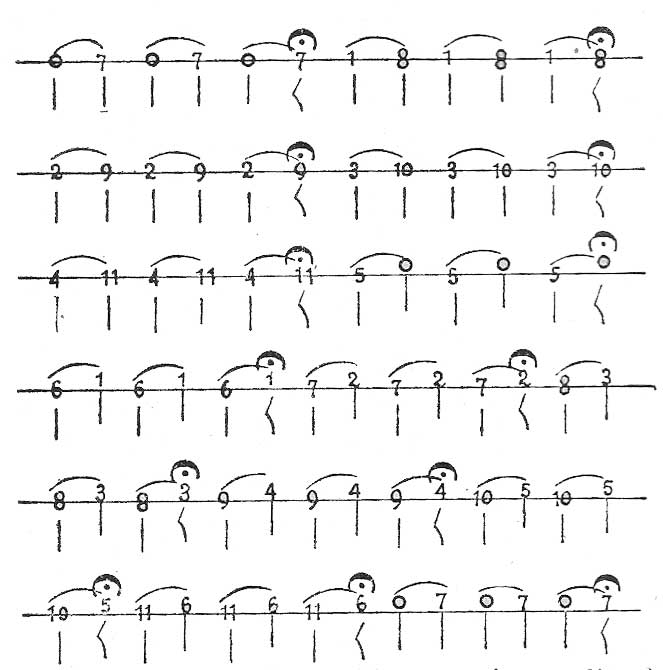
Novena, entre nueve sonidos sucesivos saltando siete, como de 0 a 8, de 1 a 9, de 2 a 10, de 3 a 11, etc.
EJEMPLO H
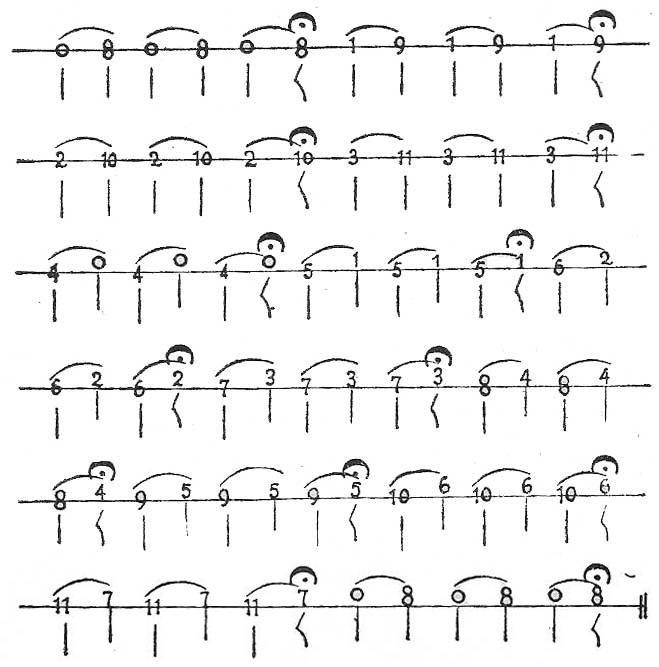
Décima, entre diez sonidos sucesivos, saltando ocho, como de 0 a 9, de 1 a 10, de 2 a 11, etc.
EJEMPLO I
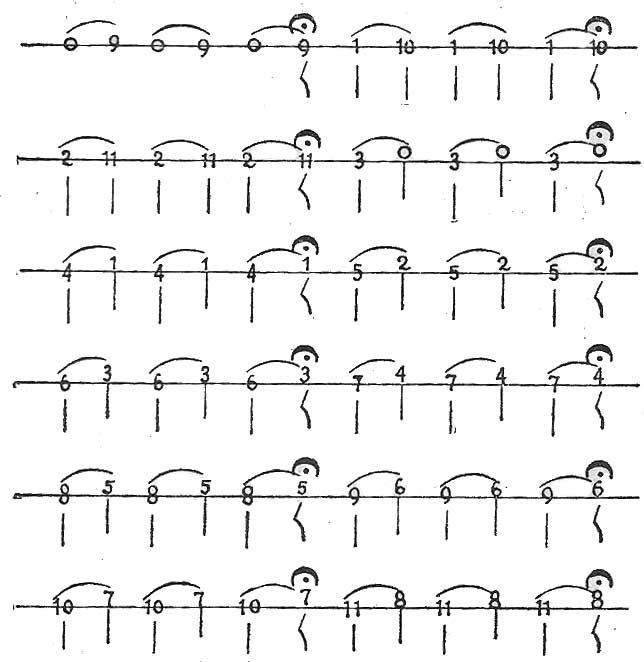
Onceava, entre once sonidos sucesivos saltando nueve, como de 0 a 10, de 1 a 11, de 2 a 0 (superior), etc.
EJEMPLO J
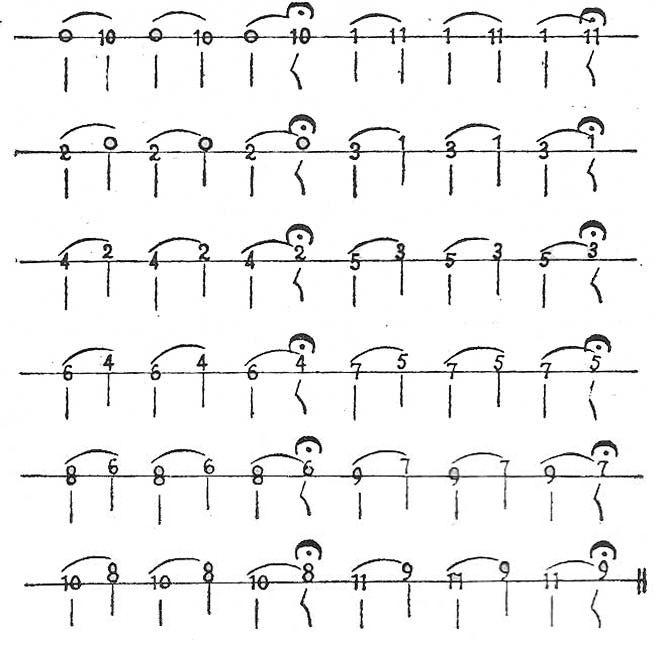
Doceava, entre doce sonidos sucesivos saltando diez, como de 0 al 11, de 1 a 0 (superior), de 2 a 1 (superior), etc.
EJEMPLO K
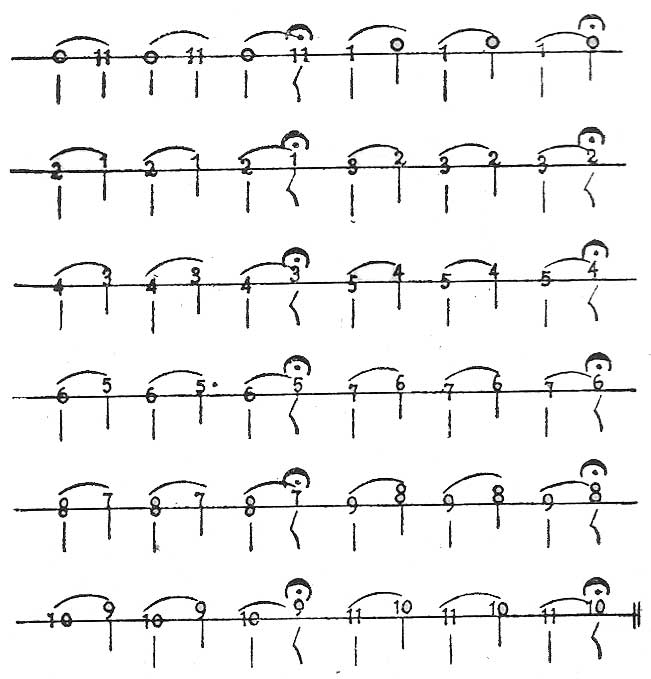
Treceava, entre trece sonidos sucesivos saltando once, como de cualquier número a su duplo superior o inferior.
EJEMPLO L
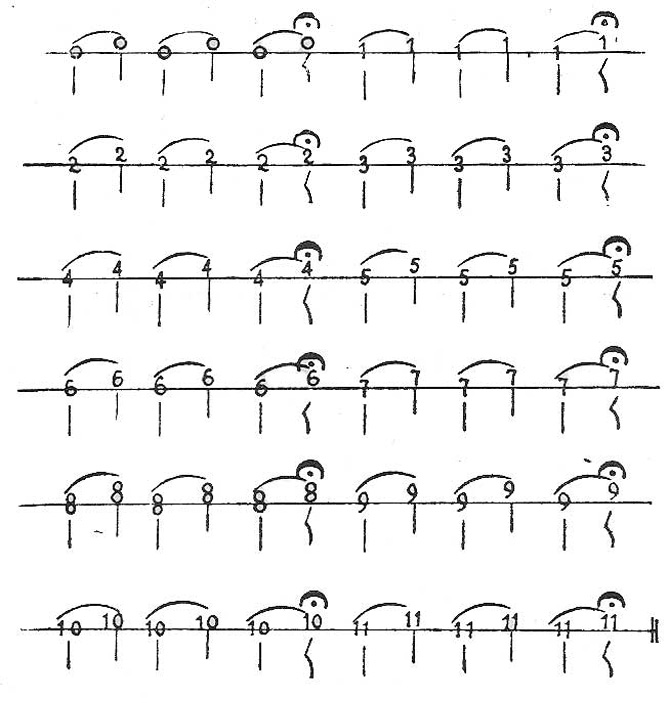
El estudiante debe fijarse en que la 13ª se produce entre cualquier sonido y su duplo superior o inferior (duplos son los sonidos representados por el mismo número, aunque estén en diversos ciclos).
Para no confundir a los estudiantes, no me referiré a todos los absurdos que se enseñan en la “Teoría Clásica de la Música” en relación con los intervalos, y concreto el comentario a las cuantas palabras que se han leído.
Para facilitar las entonaciones de los diversos intervalos, muy útil será el “Carrillófono”, instrumento que servirá no sólo para estudiar las entonaciones fáciles, sino también las muy difíciles, y por lo mismo será utilísimo para que los cantantes de profesión estudien óperas, oratorios, romanzas, etc.
Entónense muy lentamente las segundas del ejemplo A; las terceras del B; las cuartas del C; las quintas del D; las sextas del E; las séptimas del F; las octavas del G; las novenas del H; las décimas del I; las onceavas del J; las doceavas del K; y las treceavas del L.
INVERSIÓN DE INTERVALOS
Los intervalos se invierten llevando el sonido bajo a su duplo superior, o el alto al inferior.
EJEMPLO 21

Como se ve, en uno u otro caso, el resultado es el mismo, aunque en otro ciclo.
EJEMPLO 22
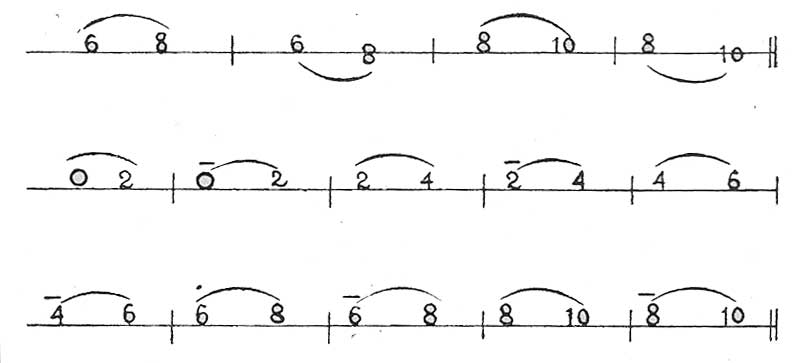
Un intervalo y su inversión, deben sumar doce dozavos.
EJEMPLO 23
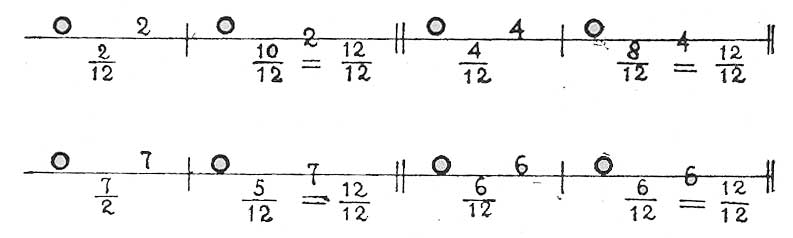
Con estas reglas aplicadas cuidadosamente, y practicadas con todo el empeño que merecen, bastará para poder entonar sin dificultad cualquiera melodía.
Una vez que se hayan practicado concienzudamente los intervalos, entonándolos, estudiaremos los medios para indicar la duración de ellos. Para terminar esta lección, entónense como en las anteriores, el Himno Nacional.
QUINTA LECCCIÓN
Duración de los sonidos.
Son siete las figuras con que se indican las duraciones de los sonidos y se llaman unidad, mitad, cuarto, octavo, dieciseisavo, treintidosavo y sesenticuatravo.
Ejemplo 24.
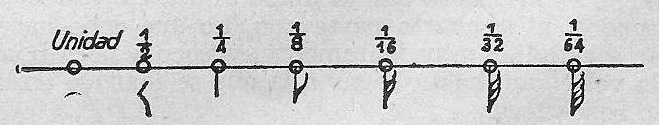
Las mismas siete figuras SIN LOS NÚMEROS, indican duración de tiempo, pero NO SONIDO.
He aquí la relación matemática de las siete figuras.
La unidad cuando representa sonido y duración, se escribe con cualquiera de los doce números PERO SIN NINGUNA LÍNEA O ADITAMENTO, y durará como dije ya, cuatro segundos.
Cuando se represente el valor de la unidad sin indicar sonido se indicará con el número uno sobre una línea diagonal; si el silencio es de doble duración que la unidad, se escribe un número dos sobre la línea diagonal; si es de tres veces el valor de la unidad, con el número tres, etc. En todas las demás figuras que indican sólo duración, bastará suprimir los números sobre ellas para saber que indican duración pero no sonido.
En la práctica –y especialmente al principio de los estudios- bastará una sola regla: marcar con golpecitos en cualquier mueble, las relaciones de las figuras entre sí, TOMANDO COMO BASE LA DE MENOR VALOR Y PROPORCIONALMENTE CON ESA FIGURA MÁS CORTA SE DARÁN A LAS DEMÁS SUS VALORES RESPECTIVOS. Si la figura más corta es un sesenticuatravo, el treintidosavo valdrá dos percusiones; el dieciseisavo valdrá cuatro; el octavo ocho; el cuarto dieciséis; el medio treinta y dos y la unidad sesenta y cuatro. Si la nota más corta fuere un dieciseisavo, el octavo valdrá dos; el cuarto cuatro, el medio ocho y la unidad dieciséis, y así en todos los demás casos.
Durante el estudio, NO ES INDISPENSABLE DAR A CADA COMPÁS SU DURACIÓN MATEMÁTICA EXACTA; es decir, no es necesario que la unidad dure exactamente cuatro segundos, ni la cuarta parte uno. Lo que debe hacerse es empezar a estudiar muy lentamente, y poco a poco ir aumentando la velocidad, hasta llegar a la que se marque en la composición respectiva.
El Himno Nacional seguirá siendo nuestra guía.
He aquí una vez más el canto patrio.
Ejemplo 25.
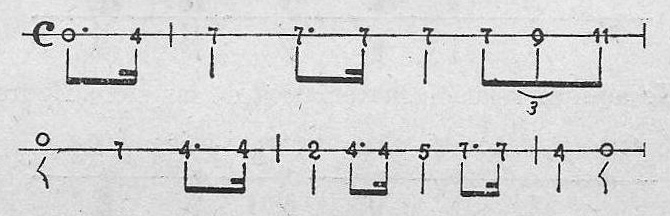
Como se ve en el ejemplo anterior, la figura más corta es la de 1/16, lo que quiere decir que cada percusión que se marque valdrá exactamente eso 1/16.
Practíquense en el ejemplo que sigue los valores de acuerdo con la regla anterior.
Ejemplo 26.
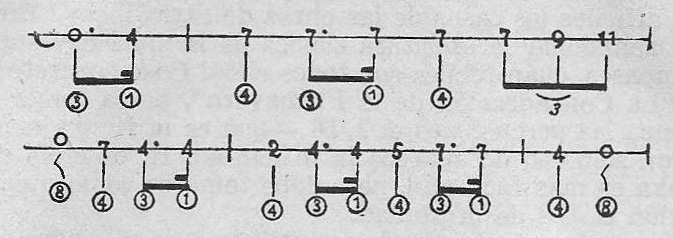
Indico entre paréntesis las percusiones que corresponden a cada figura.
COMPÁS
Llámase compás, a la división simétrica de una frase musical en X partes. ½ indica la mitad de la unidad; ¾ tres cuartas partes; ¼ la cuarta parte; 3/8 tres octavos, 9/8 indica nueve octavos de la unidad; 12/8, doce octavos de la unidad; 5/4 cinco cuartos de la unidad, etc., etc.
En cada caso hay que poner las figuras necesarias para llenar el lapso que indica el compás, y después de ellos una línea vertical u oblicua.
Ejemplo 27.
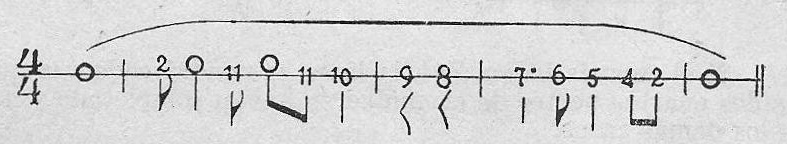
Tengo la firme creencia de que, de igual modo que no fue posible avanzar en la conquista de los sonidos mientras se conservaron los nombres de las notas y las pautas, llaves y accidentes, no se avanzará en el ritmo, mientras no se abandonen los compases. Demostración clara de esta tesis, la veo en los casos que pongo en el ejemplo final de este “Método”; pues marcando el compás en cada uno de ellos, son dificilísimos y en cambio SUPRIMIENDO LAS LÍNEAS DIVISORIAS DE COMPÁS SON MUY FÁCILES. Hasta los ejemplos rítmicos de Stravinsky resultan de increíble facilidad.
Todos los casos del ejemplo que pongo en el final de este “Método”, han sido considerados como difíciles. ¡Cuán difícil fue el de Schumann! ¡Cuán difícil el de la Sinfonía Patética de Tchaikovsky! ¡Cuán difícil es el pasaje de contrabajos de la 9ª Sinfonía de Beethoven! Y sobre todo ¡qué enormemente difíciles los casos de las obras de Stravinsky! En cambio, al abandonar la escritura clásica de la música y suprimir los compases, ¡cuán fáciles son todos ellos! Caso concreto: para el de “La Consagración de la Primavera”, basta tomar como base para las percusiones el 1/16 que es la figura más corta y con solo eso desaparece la dificultad. El ejemplo de Petrouchka es más fácil aún, pero debe tomarse como unidad de percusión el 1/8 de la unidad.
La regla anterior puede ser utilísima no sólo para los que empiecen a estudiar, sino también para muchos directores de orquestas sinfónicas.
La unidad puede indicarse de muy diversas maneras (para quien haya profundizado un poco la aritmética, muy fácil será encontrar miles y miles de combinaciones para completar el valor de la unidad) 2/2, 3/3, 4/4, 5/5, etc. En el sistema musical clásico no existen figuras para dividir la unidad en tercios ni en quintos, sextos, etc. Más tarde indicaré los procedimientos artificiosos que se emplean cuando esos casos se presentan. Al completar al número de figuras necesarias para el valor que marque el compás, se pondrá la línea vertical u oblicua.
Si el compás indicado al empezar es de 4/4 se colocará una línea vertical cada vez que se hayan completado cuatro cuartos de la unidad.
Ejemplo 28.
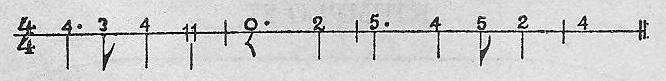
Si el compás indica 2/4, la línea se pondrá cada vez que las dos cuartas partes de la unidad se hayan completado y así de los demás casos.
Ejemplo 29.
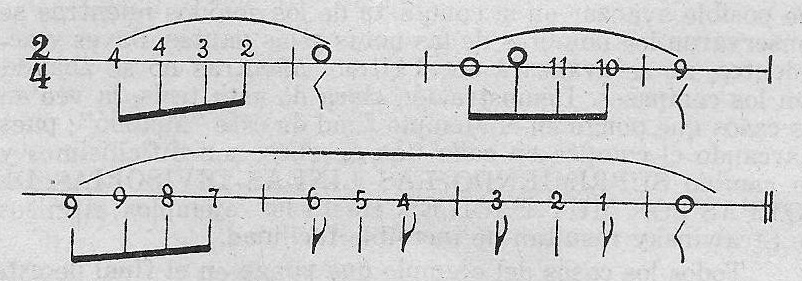
Con mi nueva gráfica, es ya casi inútil hablar de compases, pues como dije antes, las figuras solas indican sus duraciones exactas.
Ejemplo 30.

Si se canta el ejemplo anterior, se verá que esa melodía es igual sin las líneas divisorias de compás que con ellas.
Ejemplo 31.

Los pedagogos de la música no pensaron que con sus procedimientos planteaban una simultaneidad de problemas absolutamente innecesaria: 1.- leer los sonidos; 2.- entonarlos; 3.- medirlos; 4.- pensar en el compás y 5.- marcarlo con la mano. Al desaparecer los compases, quedan suprimidos en el acto dos de estos problemas, pues ya no hay que pensar en los compases ni en la manera de marcarlos con la mano, y como tampoco es ya un problema leer los sonidos, supuesto que los números del cero al once se conocen desde primer año de Escuela Primaria, desaparece uno más; y en cuanto a la medida, se estudiará más tarde, profundizándola, cuando se sepa entonar cada sonido perfectamente.
Cuando se escriben dos o más figuras de la misma especie, del 8º de unidad en adelante en vez de corcheas se emplean barras corridas para unirlas.
Una, si son octavos;
Ejemplo 32.
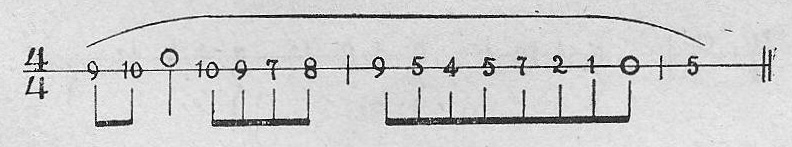
Dos, si son 16avos,
Ejemplo 33.

Tres, si son 32avos,
Ejemplo 34.

Y cuatro, si son 64avos.
Ejemplo 35.
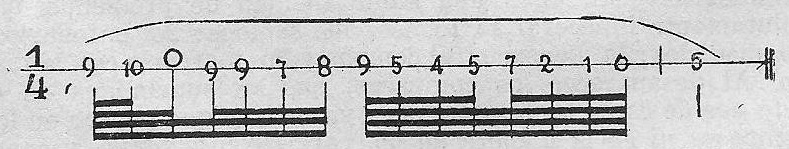
PUNTILLOS
Existen En la escritura de la música unos pequeños puntos, que aumentan las duraciones de los sonidos o los silencios, y se escriben después de cualquiera de las figuras. (Excepto del 64avo).
El puntillo aumenta a la figura que le antecede, la mitad de su valor. Si es la unidad, con puntillo valdrá seis segundos;
Si vale dos segundos, con puntillo valdrá tres;
Ejemplo 36.
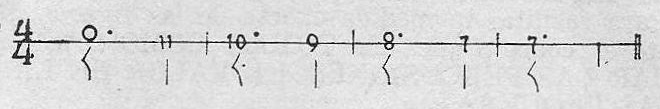
Si vale uno, con puntillo valdrá uno y medio, etc.
Ejemplo 37.
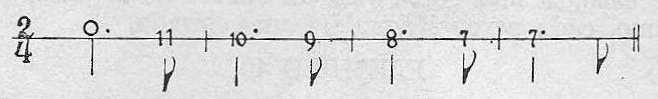
Cuando hay dos puntillos seguidos, el primero aumenta la mitad del valor de la figura, y el segundo, la mitad del primer puntillo.
Ejemplo 38.
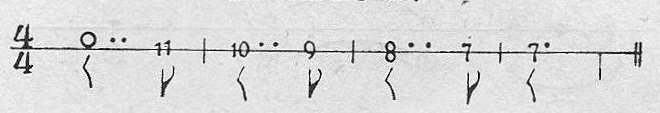
Generalmente cuando una figura lleva puntillo, le sigue otra de menor valor; es decir, que después de una mitad con punto va un cuarto; después de un cuarto con punto va un octavo, etc. Sirviéndose de los puntillos, se multiplican los elementos para las combinaciones de figuras entre sí; ya sea que se trate de la unidad o de cualquiera de las otras figuras.
Ejemplo 39.
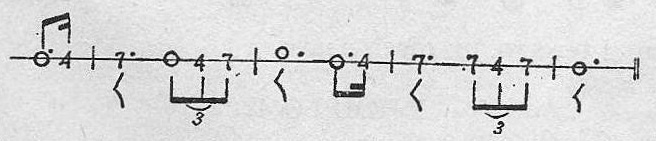
Bastan las explicaciones dadas, para poder medir los sonidos musicales, tomando una vez más como base, el canto patrio, y así cuando se haya terminado de estudiar este “Método”, muy fácil será cantar cualquiera melodía por complicada que fuere.
Como primer ejercicio, practíquese la medida en el Himno Nacional, pero sin cantar, y cuando ya estén las figuras bien medidas, entonces cántese y mídase simultáneamente.
En este caso, para practicar la medida, sigue en pie mi tesis: IR DE LO CONOCIDO A LO DESCONOCIDO.
Para facilitar la medida exacta de las figuras, téngase presente el consejo que dí: TOMAR COMO BASE PARA MARCAR LAS PERCUSIONES, EL VALOR DE LA FIGURA MÁS PEQUEÑA.
Ejemplos para la práctica
He aquí el Himno Nacional, en diversas figuras. En el primer caso, la más corta vale un cuarto de la unidad, y por lo mismo, cada percusión valdrá un segundo.
Ejemplo 40.
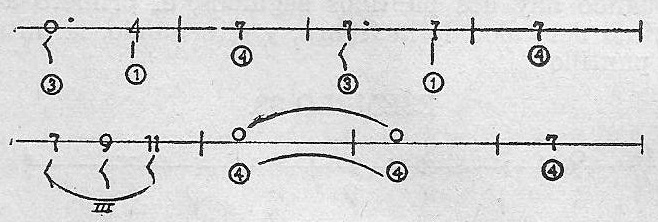
En el segundo, vale un octavo de la unidad,
Ejemplo 41.
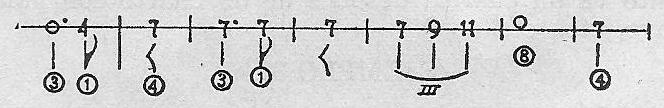
En el tercero, un dieciseisavo,
Ejemplo 42.
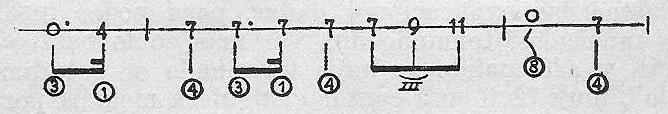
En el cuarto un treintidosavo,
Ejemplo 43.
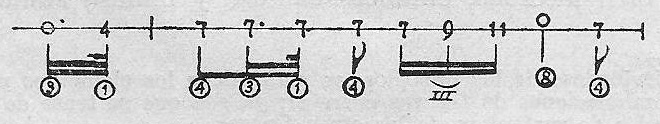
Y en el quinto un sesenticuatravo.
Ejemplo 44.

En el quinto compás del ejemplo 40, hay un grupo de tres figuras que deben cantarse en el mismo tiempo que sólo dos de ellas; se llama tresillo y se indica con una pequeña línea curva con un número 3 afuera de la línea.
VALORES IRREGULARES
Para simplificar la medida exacta de esos valores que los músicos llaman irregulares, aconsejo que se marquen tres percusiones en cada una de las cuatro partes de la unidad, dando tres a cada una de las cuatro partes de ella. He aquí la unidad dividida en cuatro partes,
Ejemplo 45.
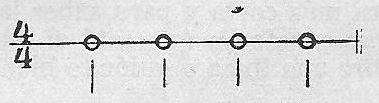
Y al marcarse el compás con la mano, según se acostumbra, es gráficamente así:
Ejemplo 46.
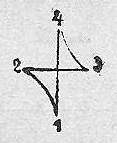
Y en seguida, cada cuarta parte subdividida en tres,
Ejemplo 47.

Es gráficamente así:
Con esto se facilita muchísimo la división de la unidad en tres partes iguales: la primera empieza en el 1 y termina en el 4; la segunda, va del 5 al 8 y la tercera del 9 al 12. Lo que explica claramente el ejemplo anterior.
Aconsejo que se practiquen esos casos cantando con los diversos valores, primero muy lentamente y poco a poco más aprisa.
SONIDOS SUCESIVOS
Daré ligeras explicaciones para leer los acompañamientos de las melodías.
En las composiciones para piano, generalmente la mano derecha hace la melodía y la izquierda el acompañamiento, y esos sonidos de la mano izquierda con frecuencia se escriben unos sobre otros en forma vertical. Para medirlos se toma como base la figura más corta y para saber las alturas de ellos, basta ver el lugar exacto en que está el número superior; es decir, si está sobre una línea o guión, o bien en el guión, o debajo de él.
Las melodías provienen de los sonidos sucesivos, lo que puede comprobarse en el propio Himno Nacional.
Y las llamadas armonías, de simultáneos.
Ejemplo 48.
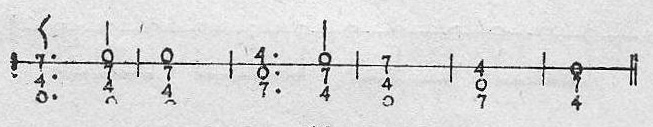
Los sonidos escritos unos sobre otros en línea vertical no puede cantarlos una sola persona, supuesto que deben oírse todos a la vez.
GRUPOS DE FIGURAS IRREGULARES
Es éste un problema ingenioso inventado por los músicos, y que tiene por fin, llenar huecos de divisiones entre unas y otras figuras.
Por ejemplo el tresillo, es para que vayan tres figuras en el mismo lapso que aritméticamente deben ir sólo dos; es decir, tres mitades en vez de dos; tres cuartos en vez de dos; tres octavos en vez de dos y tres dieciseisavos en vez de dos.
Para que se vea lo que estas figuras llamadas irregulares significan en la práctica, indicaré la unidad con sus divisiones normales, y todas las divisiones de la unidad que faltan en ellas, se llenan con esos valores a que me refiero.
Entre la unidad y el medio, no hay ninguna figura más; pero entre el medio y el cuarto, queda el tercio, que se llena con el tresillo.
Ejemplo 49.
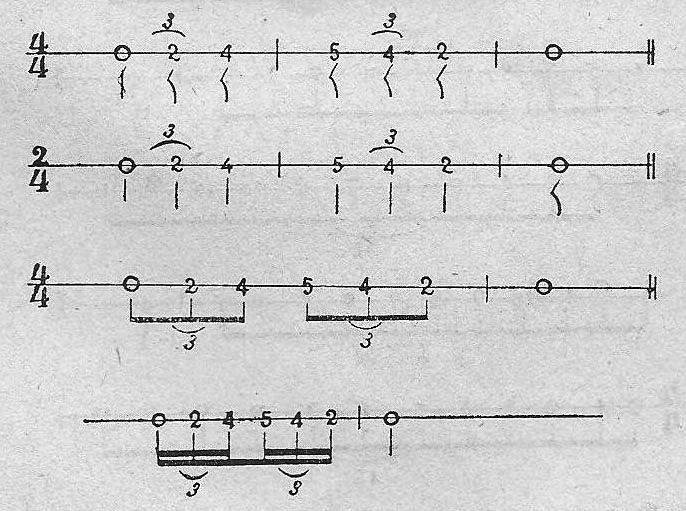
Entre el cuarto y el octavo, quedan el 5º, el 6º y el 7º que se llenan con cinco, seis o siete sonidos.
Ejemplo 50.
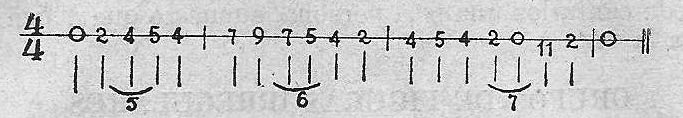
Entre el octavo y el dieciseisavo el hueco es muy grande, pues quedan el 9º, el 10º, el 11º, el 12º, el 13º, el 14º y el 15º.
Ejemplo 51.
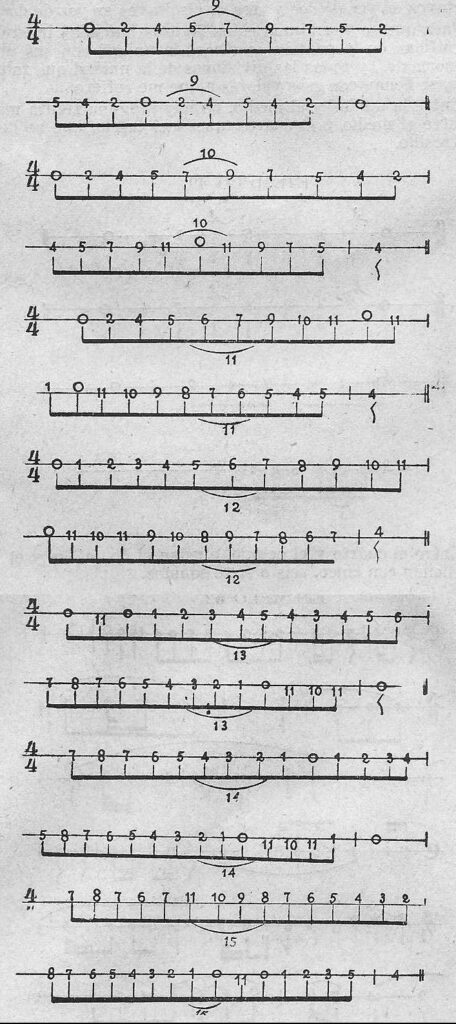
Y del dieciseisavo al treintidosavo, faltan más aún, pues se intercalan allí el 17, el 18, el 19, el 20, el 21, el 22, el 23, el 24, el 25, el 26, el 27, el 28, el 29, el 30 y el 31, y del treintidosavo al sesenticuatravo faltan todos los números progresivos hasta llegar al sesenta y cuatro.
Chopin hizo uso maravilloso de estos valores llamados irregulares, lo que se comprobará fácilmente al leer sus composiciones.
AIRES
Con las teorías expuestas, son ya innecesarios los aires, y aún los compases; pero para no alarmar a los músicos rutinarios, emplearemos en esta primera edición los compases y las líneas divisorias.
DEMOSTRACIONES PRÁCTICAS
Con lo dicho hasta aquí, basta para poder entonar y medir los ejemplos que siguen, y que son todos de las nueve sinfonías de Beethoven.
Ejemplo 52.

Practíquense cuidadosamente los casos que indico, y con eso será suficiente para aprender a entonar y medir los sonidos de la música.
Ejemplo 53.
LA GOLONDRINA

LA PALOMA
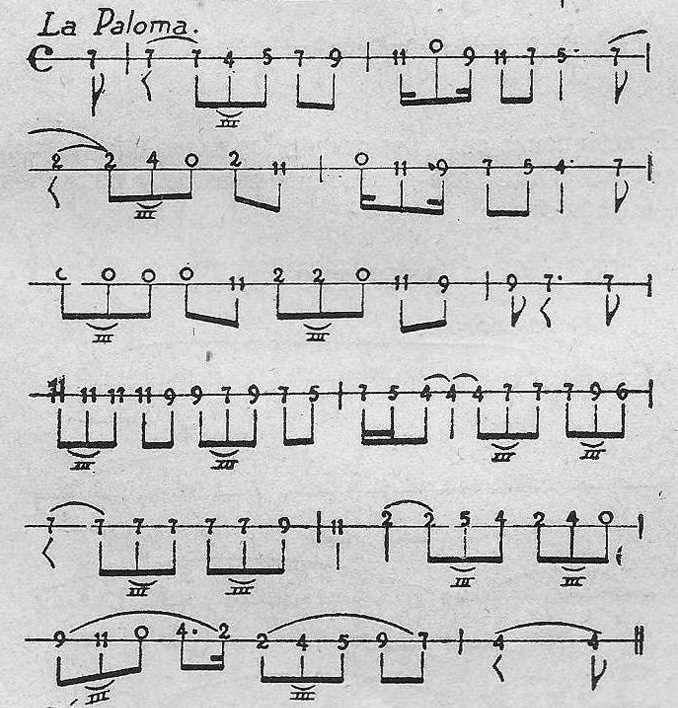
LA DIANA
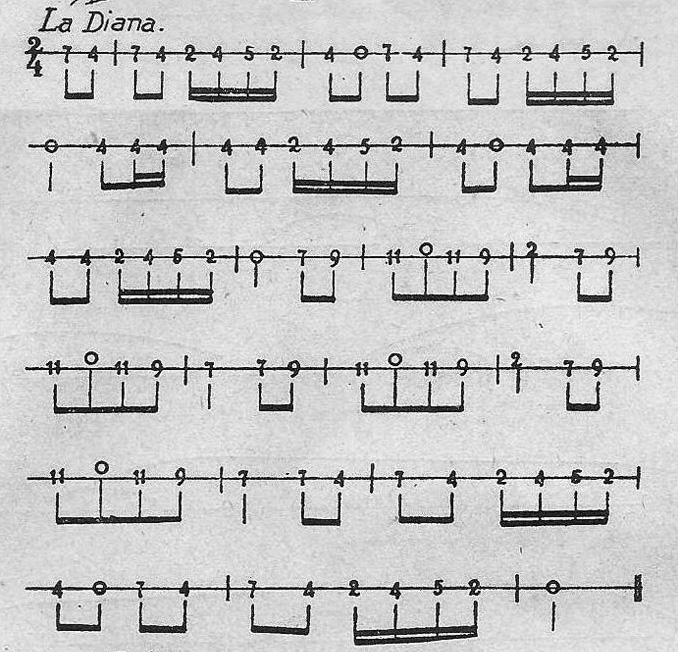
CANTO A LA BANDERA
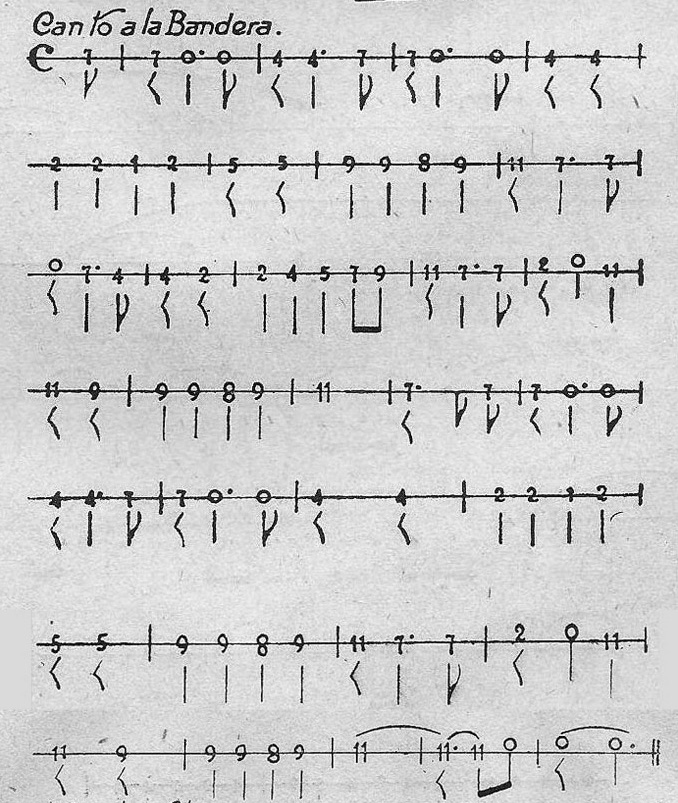
SOBRE LAS OLAS
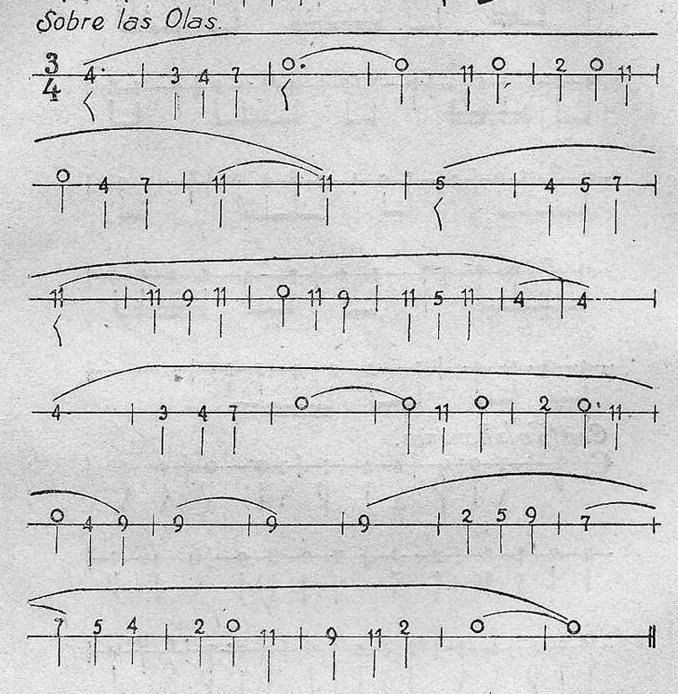
TANUHAUSER
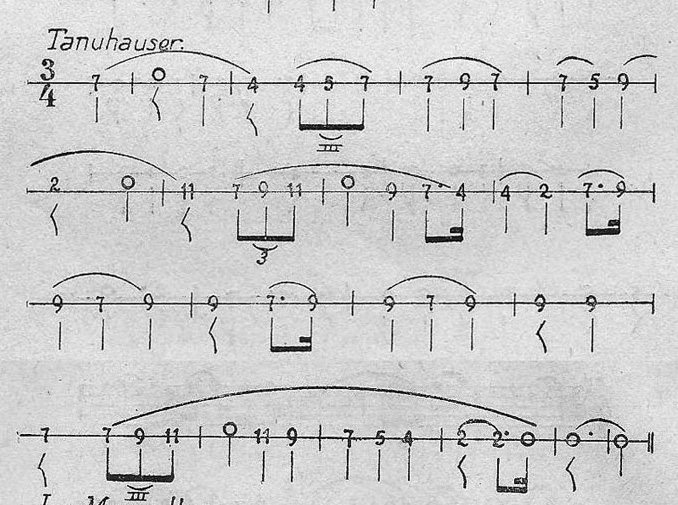
LA MARSELLESA

9a SINFONIA BEETHOVEN

PETROUCHKA. STRAWINSKY

CONCIERTO PARA PIANO. SCHUMANN

LA CONSAGRACION DE LA PRIMAVERA. STRAWINSKY

